首先看看吴恩达机器学习对评估指标的解释
1 混淆矩阵
| 混淆矩阵 | 真实值为1 | 真实值为0 |
|---|---|---|
| 预测值为1 | TP | FP |
| 预测值为0 | FN | TN |
- TP:模型预测为正类,真实也为正类。(正确的)
- FP:模型预测为正类,但真实为负类。(误报,医学上又称误诊)
- FN:模型预测为负类,但真实为正类。(漏报,医学上又称漏诊)
- TN:模型预测为负类,真实也为负类。(正确的)
2 精确率和召回率
precision = TP / (TP + FP)
recall = TP / (TP + FN)
-
note:注意区分准确率(Accuracy)和精确率(precision)
-
acc = (TP+TN) / total,是模型回答正确的比率
-
精确率和召回率都是越高越好
- 【精度:预测为正的样本中有多少是真的预测正确了(找得对)】
- 【召回:样本中的正例有多少被预测正确了(找得全)】
-
在实践中,精确率和召回率之间往往存在权衡
- 增大阈值,精确率变高,召回率变低
- 减小阈值,精确率变低,召回率变高
碰到搞不清楚的情况下,一定要从集合的角度,画韦恩图来看:

3 F1-score
F1分数是一种结合精确度和召回率的方法,但它更强调这两值中较小的那个。F1分数即为精确度和召回率的调和均值:
4 ROC曲线
来历:
ROC曲线最早运用在军事上,后来逐渐运用到医学领域。相传在第二次世界大战期间,雷达兵的任务是死死地盯住雷达显示器,观察是否有敌机来袭。理论上讲,只要有敌机来袭,雷达屏幕上就会出现相应的信号,但是实际上,有时如果有飞鸟出现在雷达扫描区域时,雷达屏幕上有时也会出现信号。这种情况令雷达兵烦恼不已:如果过于谨慎,凡是有信号就确定为敌机来袭,显然会增加误报风险;如果过于大胆,凡是信号都认为飞鸟,又会增加漏报的风险。每个雷达兵都竭尽所能地研究飞鸟信号和飞机信号之间的区别,以便增加预报的准确性。但问题在于,每个雷达兵都有自己的判别标准(阈值),有的雷达兵比较谨慎,容易出现误报;有的雷达兵则比较胆大,容易出现漏报。
为了研究每个雷达兵预报的准确性,管理者汇总了所有雷达兵的预报特点,特别是他们漏报和误报的概率,并将这些概率画到一个二维坐标里面。这个二维坐标的纵坐标为敏感性,即在所有敌机来袭的事件中,每个雷达兵准确预报的概率。而横坐标则为特异性,表示了在所有非敌机来袭信号中,雷达兵预报错误的概率。由于每个雷达兵的预报标准不同,且得到的敏感性和特异性的组合也不同。将这些雷达兵的预报性能进行汇总后,管理者发现他们刚好在一条曲线上,这条曲线就是我们经常在医学杂志上看见的ROC曲线。
定义:
受试者工作特征曲线 (receiver operating characteristic curve,简称ROC曲线)。受试者工作特征曲线就是以假阳性概率(False positive rate)为横轴,真阳性(True positive rate)为纵轴所组成的坐标图,和受试者在特定刺激条件下由于采用不同的判断标准得出的不同结果画出的曲线。
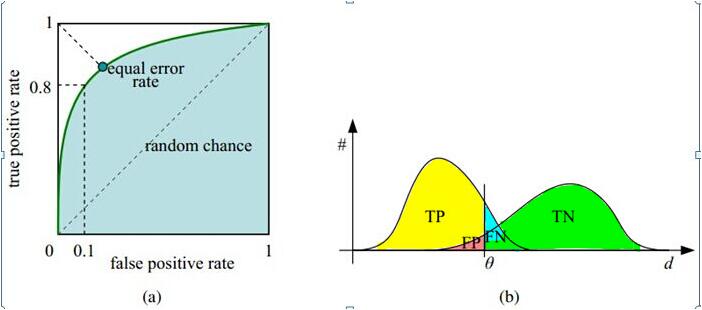
- 图(a)中,我们希望TP越多越好,但一味减小阈值(图b中对应θ向右移动,这里方向有点问题但问题不大),FP也会增多。图中(0,0)点表示啥也不报,(1,1)点表示啥都报。
- 图(b)中,左波为真实1,右波为真实0。θ左侧模型预测为1,右侧预测0。黄色TP,红色FP,蓝色FN,绿色TN,注意颜色有交集。
TPR = TP / (TP + FN) = recall = TP/真实1 = TP占左波的面积
FPR = FP / (FP + TN) = FP/真实0 = FP占右波的面积
TNR = 1 - FPR = TN / (FP + TN)
作用:
-
选择最佳的阈值。ROC曲线最靠近左上角的点是错误最少的最好阈值,其假阳性和假阴性的总数最少。理想情况TPR=1,FPR=0,故ROC曲线越靠拢(0,1)点,越偏离45度对角线越好。
-
不同模型之间的识别能力的比较。将不同模型的ROC曲线绘制到同一坐标中,越靠近左上角的ROC曲线所代表的最准确。也可通过计算ROC曲线下的面积(AUC)进行比较,越大模型越好。


